img

Word2Vec

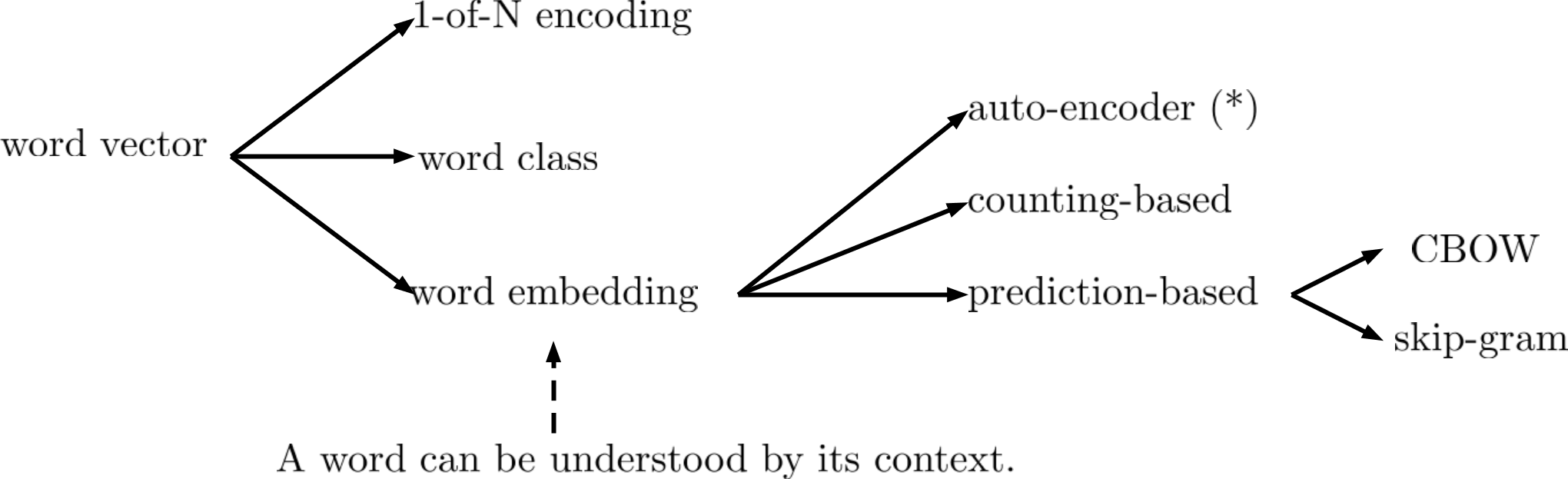
Word2Vec有以下几种方式：

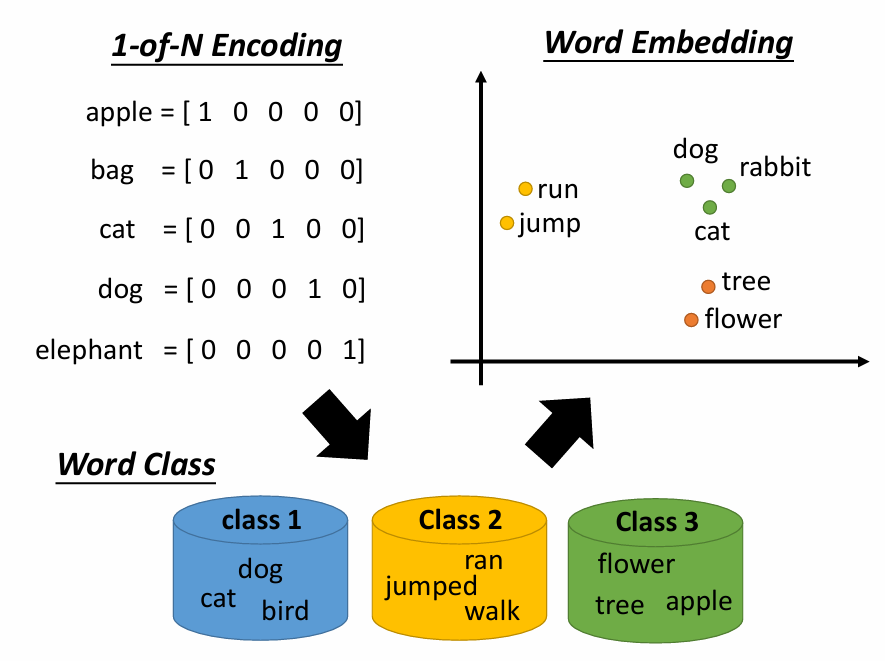
1-of-N Encoding：vector中元素的数量=word的数量，对一个单词来说只要vector中对应元素为1，其他元素为0 。但这种表示方式无法建立word之间的联系

Word Class：把具有相同性质的word进行聚类划分成多个class，用word所属的class表示该word。但聚类算法强迫每个样本属于并只属于一个cluster，实际上一个样本会有多个cluster的特征，比如dog的class是动物，flower的class是植物，但它们又同属于生物

Word Embedding：把所有word投影到一个空间，且该空间的维度远低于1-of-N Encoding，这是一个Dimension Reduction的过程。语义相近的word在该投影空间中是比较接近的，且该空间的每一维都有特殊的含义。

image-20260219170806232

Word Embedding是一个无监督的方法，只要让机器阅读大量文章，它就可以知道每一个word在embedding之后的特征向量。我们的任务就是训练一个神经网络，输入为word，输出为word对应的embedding vector。它的基本思路是根据word的上下文获取该word的含义。比如“A担任总统”与“B担任总统”，他会知道A、B前后都有相同/相似的内容，于是就可以推测A与B是类似的

如何做Word Embedding

Counting based

假设$w_i$和$w_j$这两个word经常在一篇文章中同时出现，他们的word vector分别用$V(w_i)$和$V(w_j)$表示，则$V(w_i)$和$V(w_j)$会比较接近。假设$N_{i,j}$是$w_i$和$w_j$这两个词汇在相同文章中同时出现的次数，我们希望它和$V(w_i)·V(w_j)$越接近越好

Prediction based

给定一个sentence，我们要训练一个神经网络，它要根据当前的word$w_{i-1}$来预测下一个可能出现的word$w_i$是什么。整个神经网络把$w_{i-1}$的1-of-N encoding当作input，经过网络的计算，output代表每个word为$w_i$的概率。经过充分训练之后，我们取该网络第一个隐藏层的输入当作word vector$V(w_i)$，用它来代表word$w_i$。

参数共享

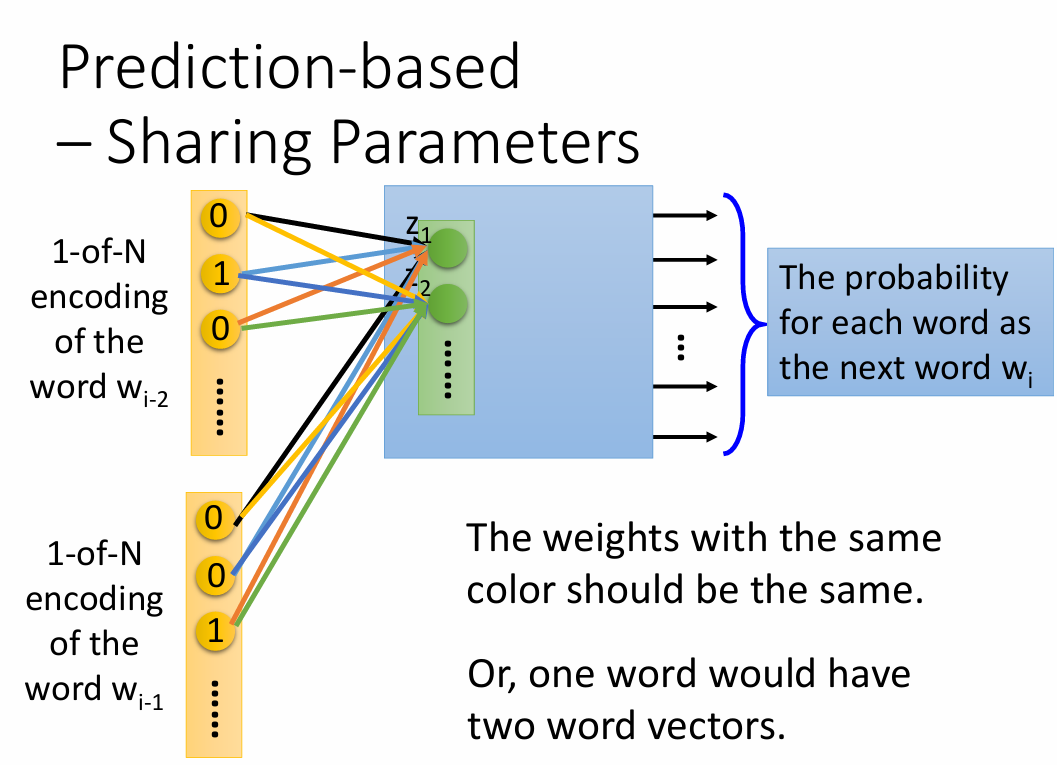
image-20260219230018672以使用2个word预测下一个word为例，在一般神经网络中直接把$w_{i-2}$和$w_{i-1}$拼接成一个更长的vector作为输入即可。如上图所示，实际上我们希望$w_{i-2}$和$w_{i-1}$的相同dimension对应的神经元中的参数是相同的，否则把同一个word分别作为$w_{i-2}$和$w_{i-1}$得到的Embedding结果会是不一样的，另外也尝试可以通过共享参数的方式有效减少参数量，不会由于输入word数量的增加导致参数量剧增。

公式定义

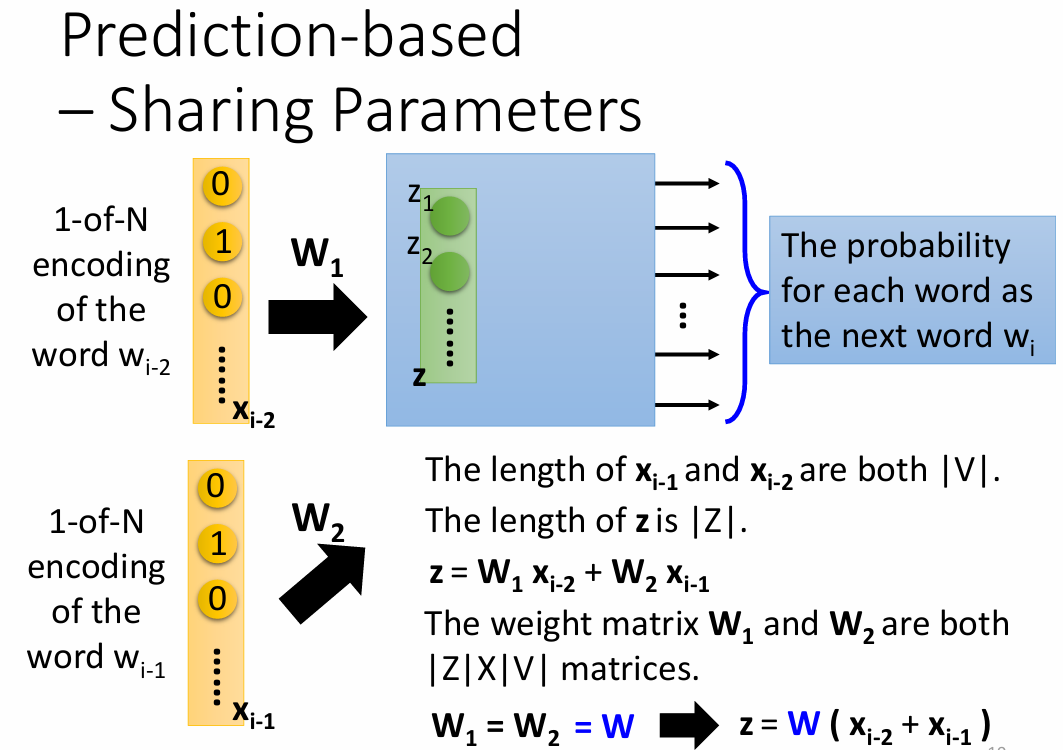
如下图所示，假设$w_{i-2}$的1-of-N编码为$x_{i-2}$、$w_{i-1}$的1-of-N编码为$x_{i-1}$,它们的维数$|V|$为数据中word的数量，隐藏层的输入向量$z=W_1x_{i-2}+W_2x_{i-1}$，其中$W_1$和$W_2$都是$|Z|$$|V|$维的weight matrix，$z$的长度$|Z|$表示降维后的维数image-20260219230231756

我们让$W_1=W_2=W$，此时$z=W(x_{i-2}+x_{i-1})$，只要我们得到了这组参数W，就可以与1-of-N编码x相乘得到word embedding的结果$z$。要使$W_1=W_2$，我们只需保证初始值相同并且更新流程相同即可，即
$$
w_i = w_i - \eta \frac{\partial C}{\partial w_i} - \eta \frac{\partial C}{\partial w_j}
$$

$$
w_j = w_j - \eta \frac{\partial C}{\partial w_j} - \eta \frac{\partial C}{\partial w_i}
$$

其它Prediction-based方法

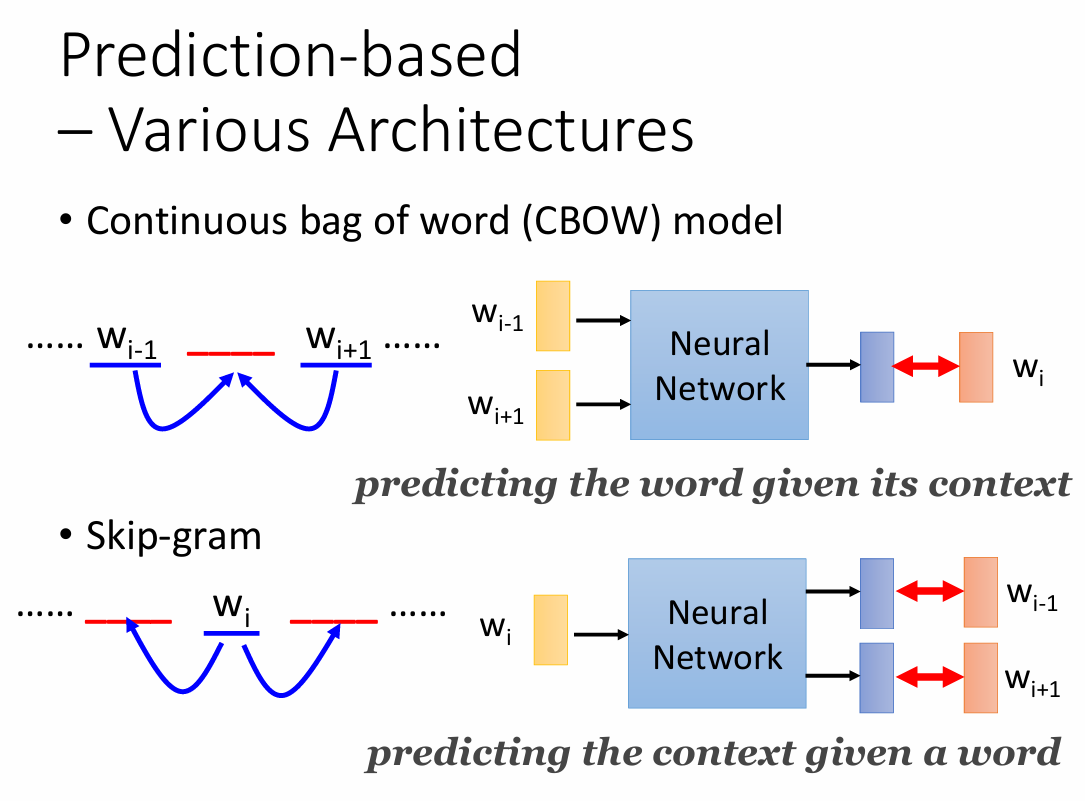
  • CBOW(Continuous bag of word model)
    拿前后的词汇去预测中间的词汇
  • Skip-gram
    拿中间的词汇去预测前后的词汇

image-20260219231155536