RNN

什么是 RNN？

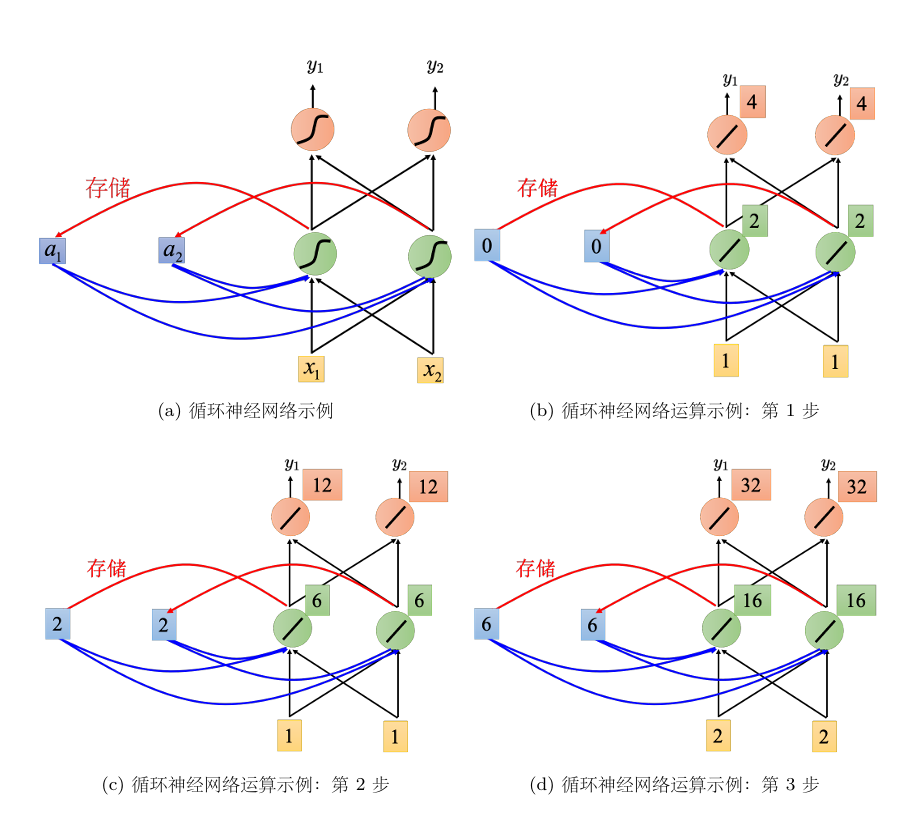
隐藏层的输出会被保留在记忆元中，在处理下一次的输入时，记忆元中的值也会被考虑。它会考虑序列的顺序，输入序列的顺序不同输出也不同。下图为权重为 1，偏置为 0，激活函数为线性的 RNN 架构处理输入序列 $[1,1]^T,[1,1]^T,[2,2]^T$ 的情况

循环神经网络运算示例

其他 RNN

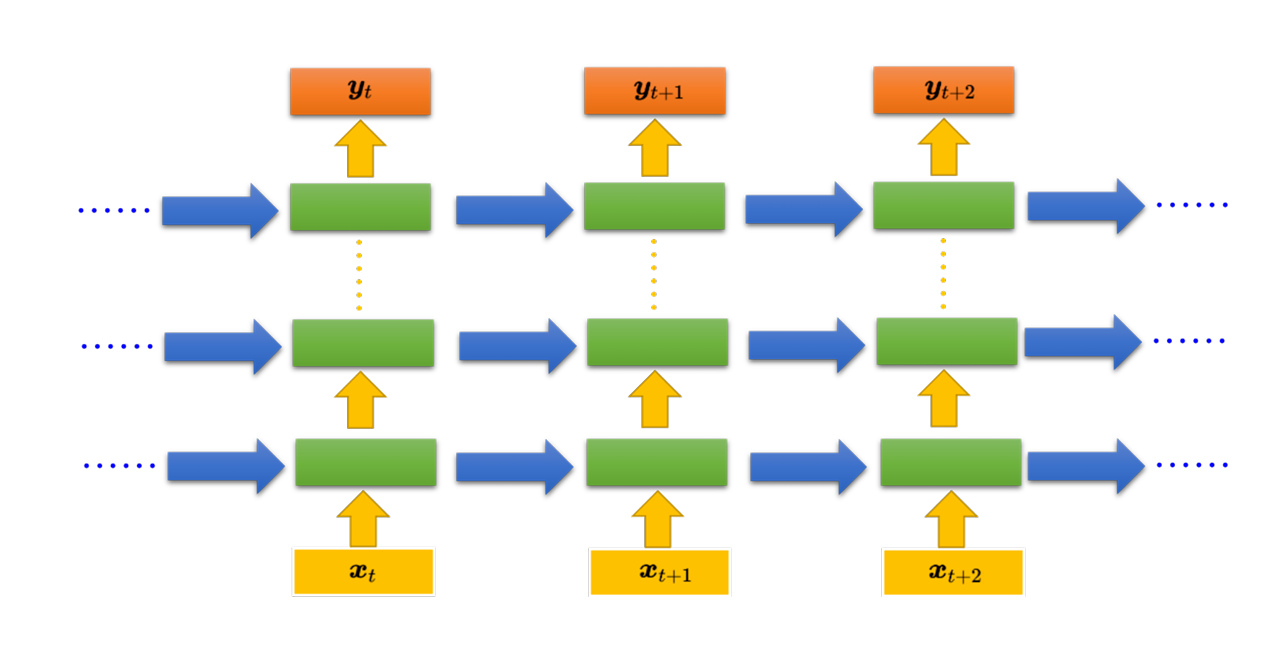
循环神经网络的架构是可以任意设计的，之前提到的 RNN 只有一个隐藏层，但 RNN 也可以是深层的。

深层循环神经网络

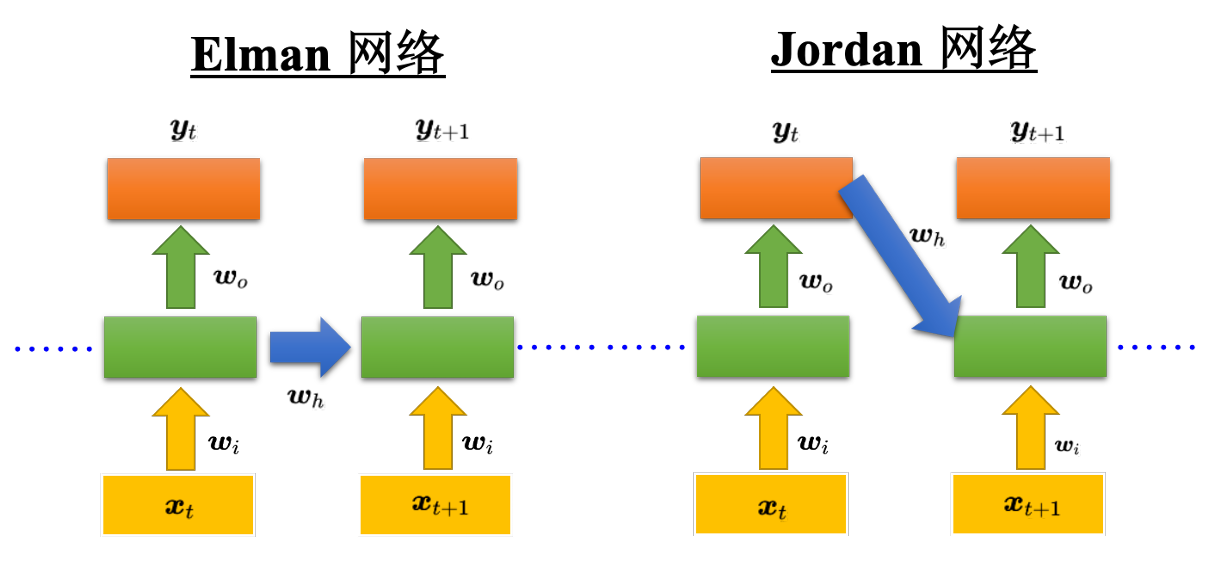
Elman 网络 &Jordan 网络

Jordan 网络存的是整个网络输出的值，它把输出值在下一个时间点在读进来，把输出存到记忆元里。Elman 网络没有目标，很难控制说它能学到什么隐藏层信息（学到什么放到记忆元里），但是 Jordan 网络是有目标，比较很清楚记忆元存储的东西。

Elman 网络和 Jordan 网络

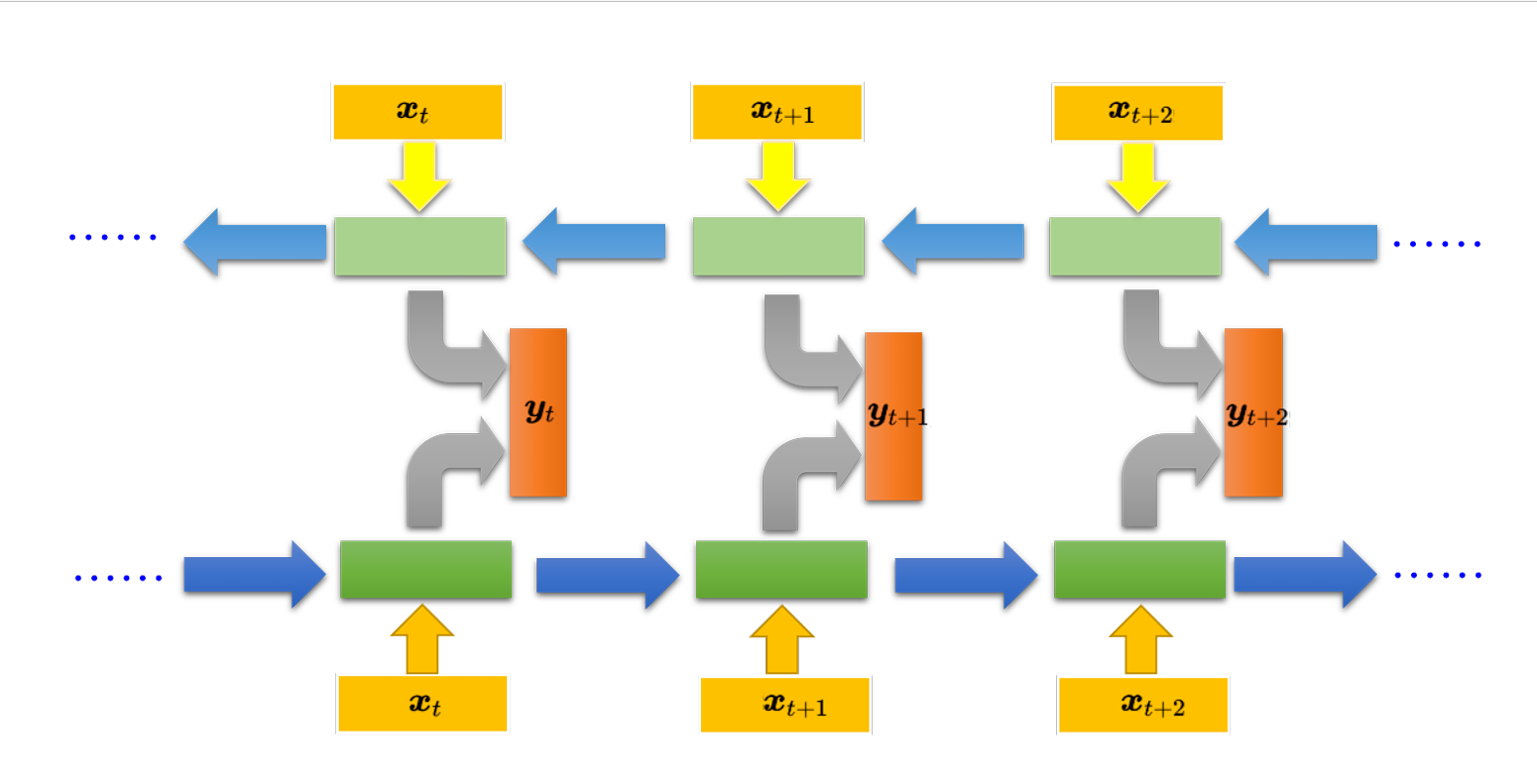
双向循环神经网络 Bi-RNN

同时训练一个正向的循环神经网络，训练一个逆向的循环神经网络，然后把这两个循环神经网络的隐藏层拿出来，都接给一个输出层得到最后的 $y_t$ 。它的好处是神经元产生输出的时候，考虑的范围是比较广的双向循环神经网络

LSTM

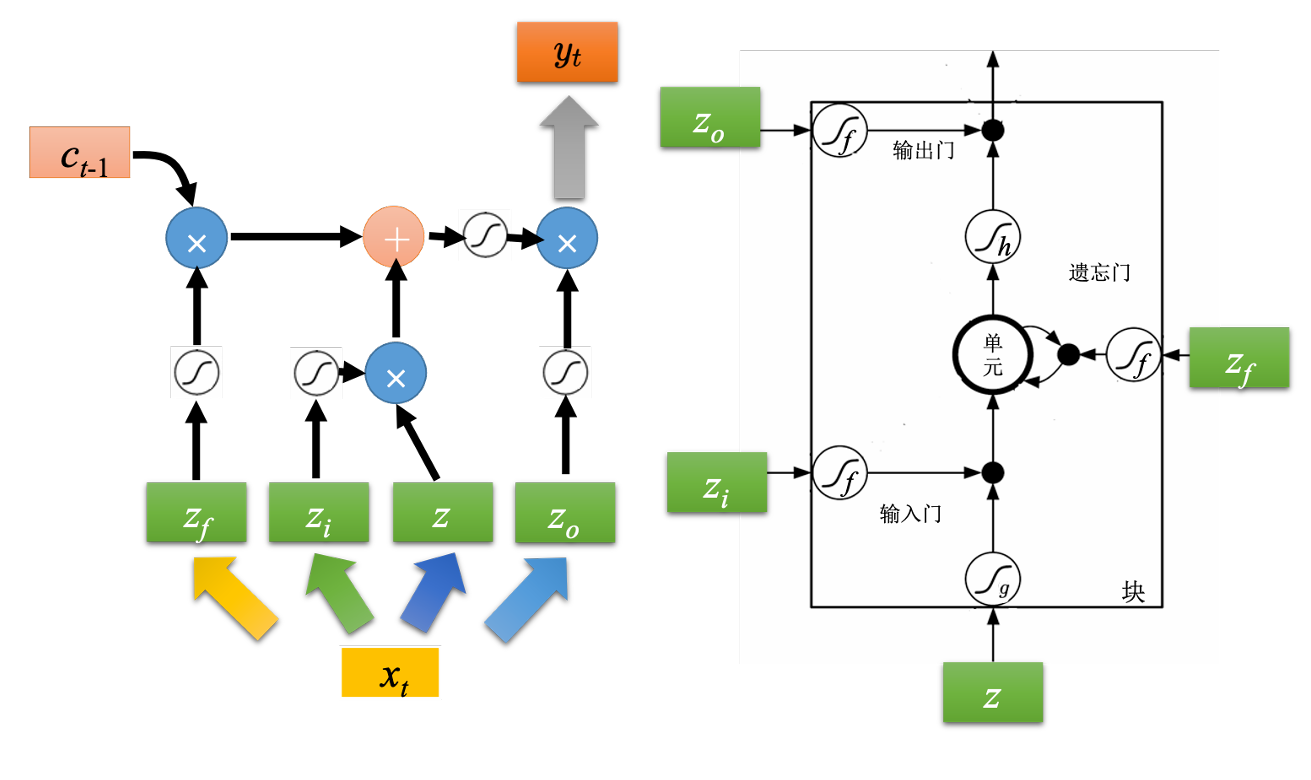
LSTM 有三个门，负责控制是否输入、清除记忆和输出

输入门: 输入门被打开时，才能把输入值写入记忆元

输出门: 输出门被打开时，外界的神经元才能把记忆元的内容读取出来

遗忘门: 遗忘门决定什么时候将记忆元的东西遗忘。当遗忘门被打开时，将输入与记忆元内容进行计算后存入记忆元。当遗忘门被关闭时，清除记忆元的内容。记忆元对应的计算公式为 $c\prime = g(z)f(z_i)+cf(z_f)$

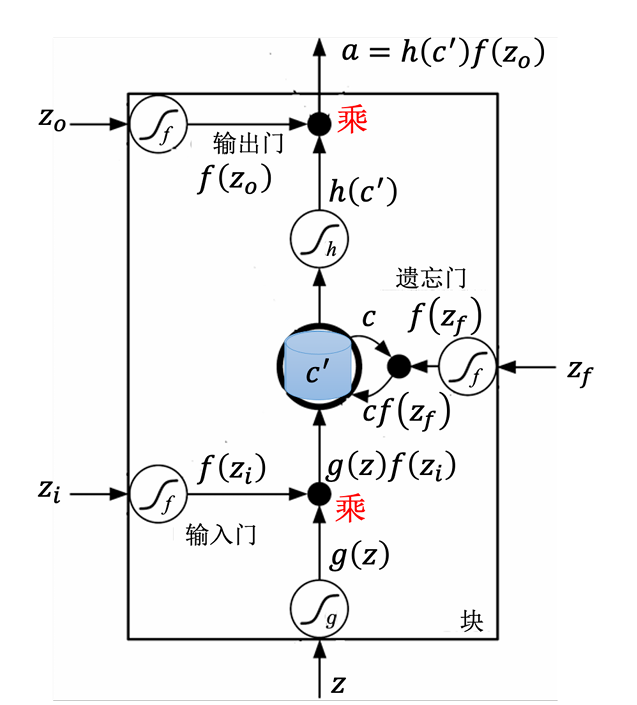
LSTM 记忆元示例

假设要被存到单元的输入为 $z$ ，操控输入门的信号为 $z_i$ ，操控遗忘门的信号为 $z_f$ ，操控输出门为 $z_o$ ，综合这些会得到一个输出记为 $a$ 。

$z$ 通过激活函数得到 $g(z)$ ， $z_i$ 通过激活函数 f 得到 $f(z_i)$ ，f 通常会选择 sigmoid 函数，因为其值介于 0~1 之间，可以表示门被打开的程度，如果 f 的输出是 1，表示门被打开的状态，反之这个门是关起来的。接下来把 $g(z)$ 乘 $f(z_i)$ 得到 $g(z)f(z_i)$ 。对于遗忘门的 $z_f$ ，也是通过 sigmoid 函数得到 $f(z_f)$ ，接下来把记忆元里的值 $c$ 乘 $f(z_f)$ 得到 $cf(z_f)$ ，相加得到 $c'=g(z)f(z_i)+cf(z_f)$ 存入记忆元中。

LSTM 原理

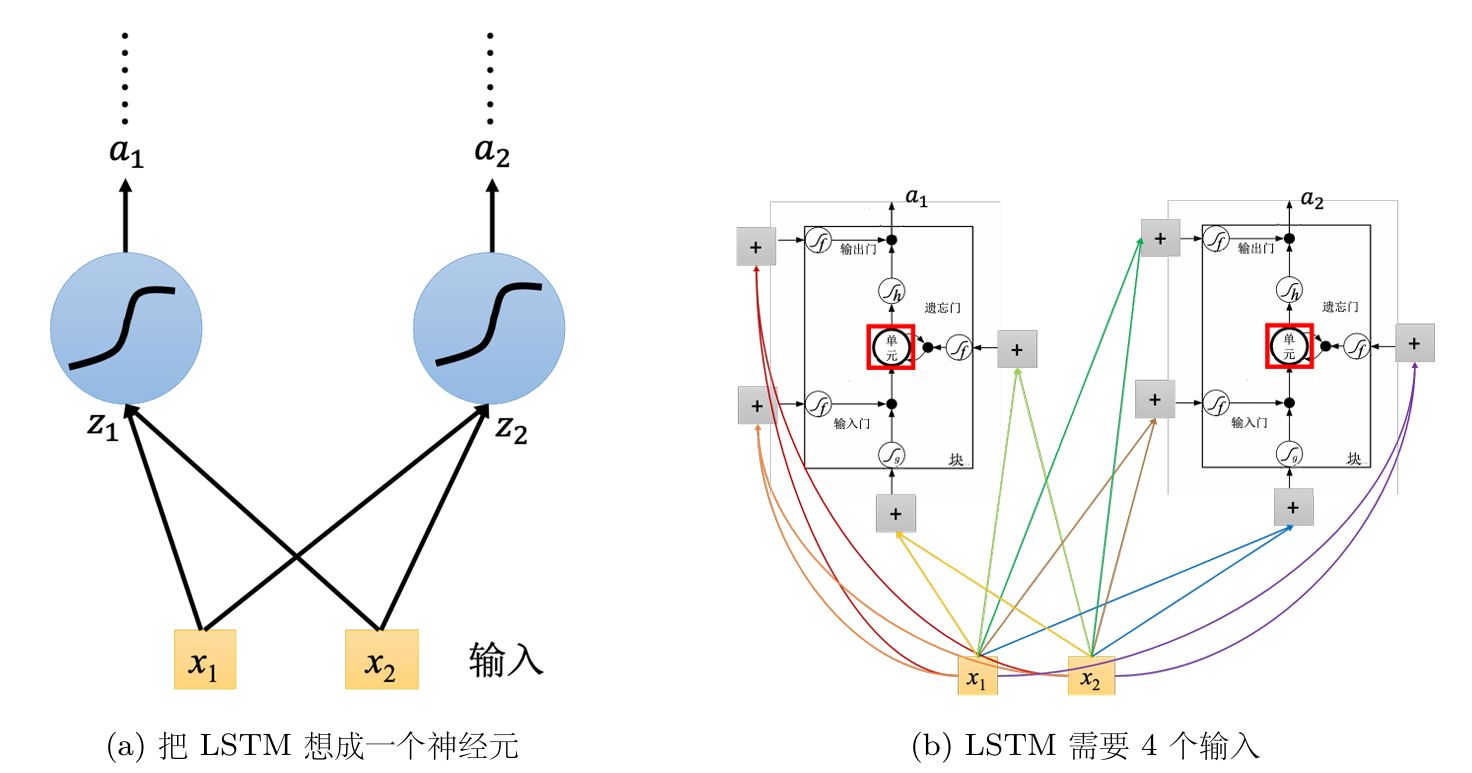
原来的神经网络里会有很多神经元，可以直接把 LSTM 当作一个神经元

LSTM 结构示意

假设用的神经元的数量跟 LSTM 是一样的，则 LSTM 需要的参数量是一般神经网络的四倍。

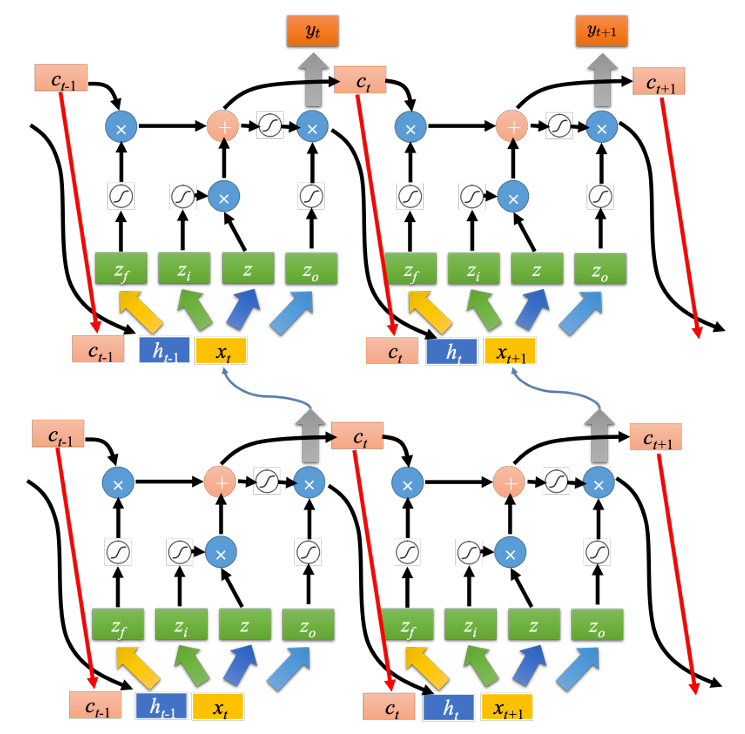
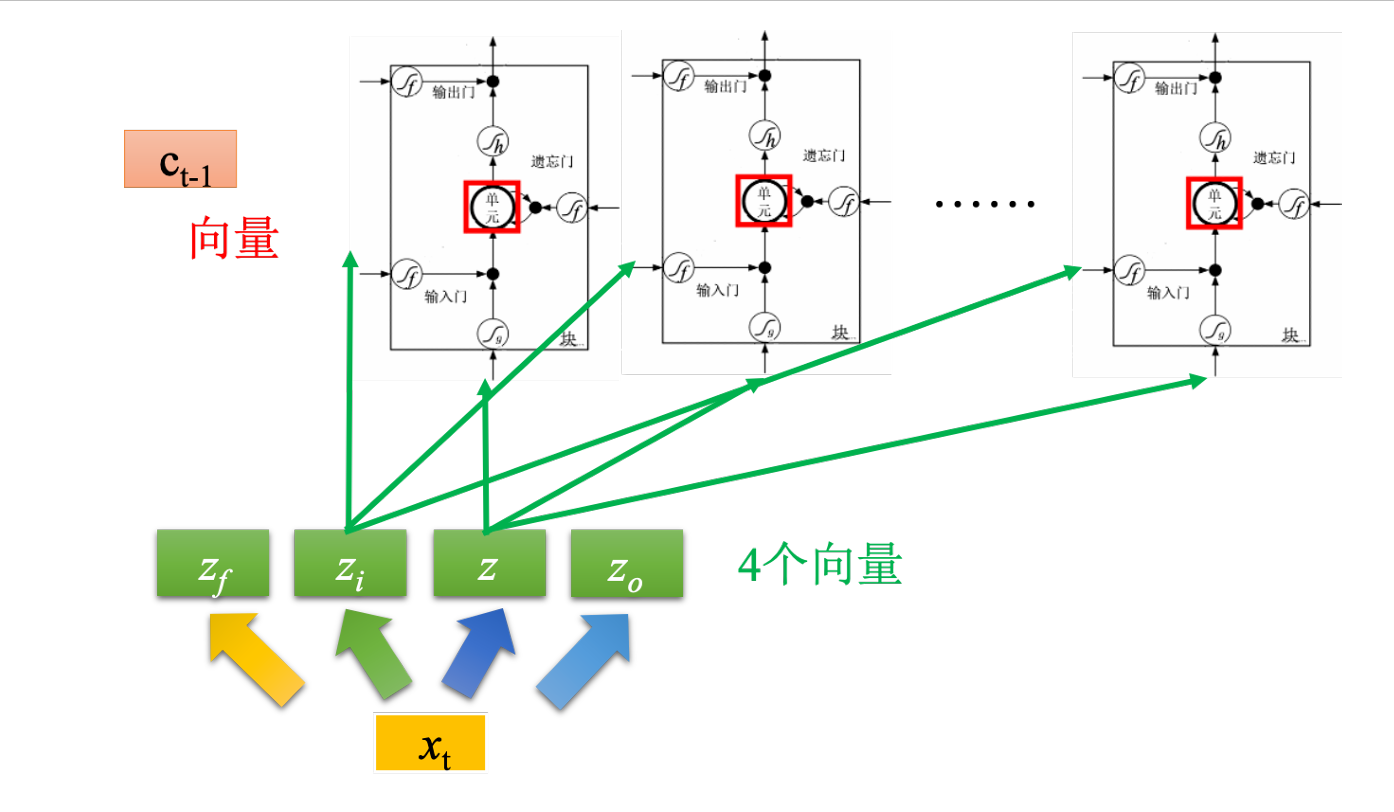
输入向量与记忆元的关系

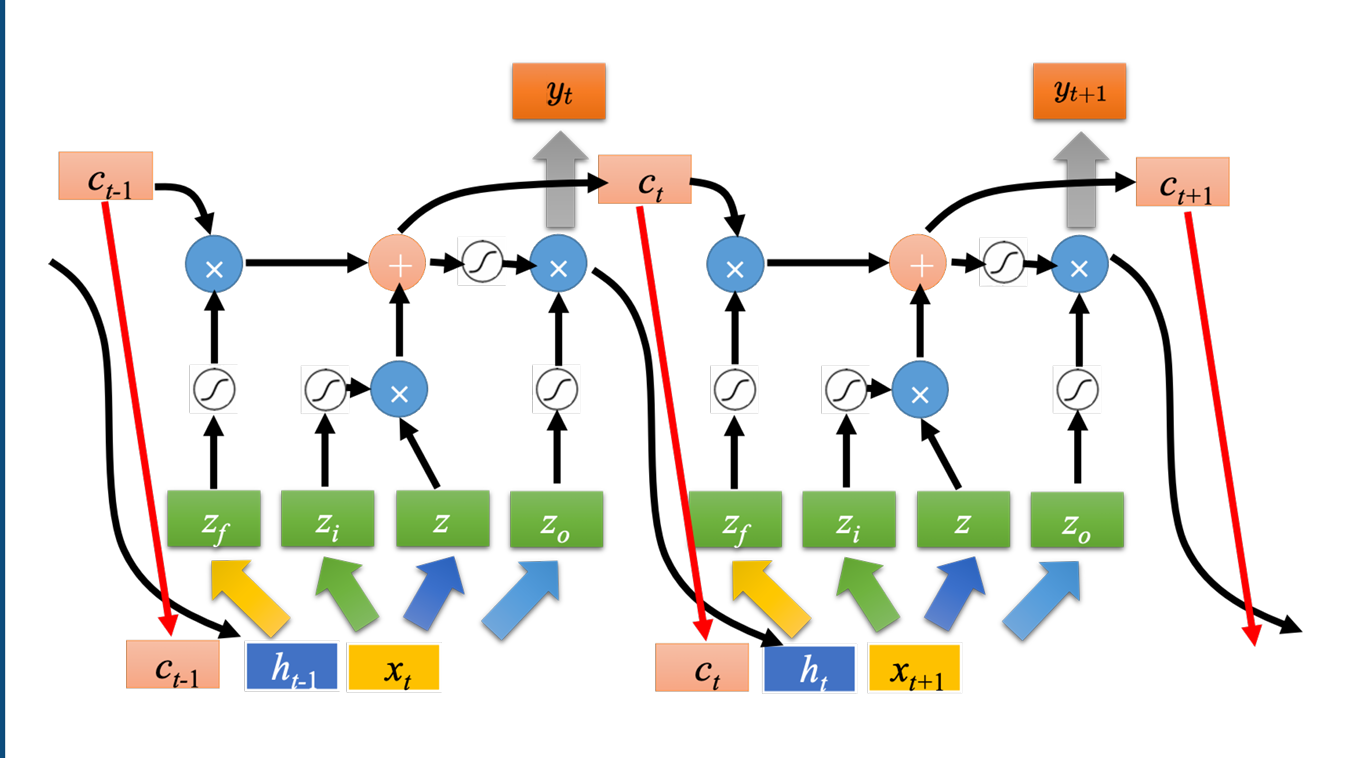
如图，假设有一排 LSTM，将所有 LSTM 的值连接起来就变成了向量，记作 $c^{t-1}$ ，现在在时间节点 $t$ ，输入向量 $x_t$ ，这个向量首先会乘上一矩阵变成一个向量 $z$ 。向量 $z$ 就代表了每个 LSTM 的输入，z 的维度刚好是 LSTM 的数量。将 $x_t$ 进行另外一次变换得到 $z_i$ ， $z_i$ 的维度也和 LSTM 单元的数量一样， $z_i$ 的每一个维度都会去操控输入门。输出门与遗忘门也是相同的道理。所以我们把 $x_t$ 进行四次不同的变换得到四个不同的向量，四个向量的维度与 LSTM 的数量一样，把这些向量合起来就会去操控这些记忆元的运作。记忆元一起运算示例

完成该时间点的操作后，继续进行下一个时间点的运算。真正的 LSTM 还会把上个时间点输出值 $h^t$ 接入当作下一个时间点的输入，并添加 peephole 连接，即把记忆元的值也拉过来。操控 LSTM 四个门的时候，同时考虑 $x_{t+1},h^t,c^t$ ，把这三个向量并在一起经过变换得到四个不同的向量再去操控 LSTM

LSTM 完全体

LSTM 通常不会只有一层

多层 LSTM 门控循环单元 GRU 是 LSTM 的简化版本，它只有两个门，但性能相近，少了 1/3 的参数，不容易过拟合。如果训练 LSTM 的时候，过拟合的情况很严重，可以尝试 GRU。它会把输入门和遗忘门联动起来，当输入门打开的时候，遗忘门会自动关闭(格式化存在记忆元里面的值)，当遗忘门没有要格式化里面的值，输入门就会被关起来。也就是要把记忆元里面的值清掉，才能把新的值放进来。

RNN 的学习方式

以槽填充为例，将 RNN 的输出与参考向量计算交叉熵，这个参考向量的长度就是槽的数量，对应的槽的值为 1，其他为 0。RNN 的损失函数输出和参考向量的交叉熵的和就是要最小化的对象

RNN 计算损失示意

使用梯度下降来进行训练，值得注意的是，RNN 的反向传播是随时间反向传播(BPTT)，需要考虑时间上的信息

但是，RNN 的训练是比较困难的，它存在梯度爆炸的情况，最简单的方法是“裁剪”，即当梯度大于某个阈值时，不要让它超过阈值 RNN 训练过程中的学习曲线与裁剪技巧

究其原因，以一个直观的例子来解释，只有一个神经元，这个神经元是线性的。输入没有偏置，输入的权重是 1，输出的权重也是 1，转移的权重是 $w$ 。也就是说从记忆元接到神经元的输入的权重是 $w$ 。经过多次迭代， $w$ 的值会被积累。所以 RNN 不好训练的原因是来自于它有时间序列同样的权重在不同的时间点被反复的使用。

如何解决 RNN 梯度消失或者爆炸

广泛使用的技巧是 LSTM。

RNN 和 LSTM 在面对记忆元的时候，它们处理的操作是不一样的。在 RNN 里面，在每一个时间点，神经元的输出都要记忆元里面去，记忆元里面的值都是会被覆盖掉。但是在 LSTM 里面不一样，它是把原来记忆元里面的值乘上一个值再把输入的值加起来放到单元里面。它的记忆和输入是相加的。LSTM 和 RNN 不同的是，如果权重可以影响到记忆元里面的值，一旦发生影响会永远都存在。而 RNN 在每个时间点的值都会被格式化掉，只要这个影响被格式化掉它就消失了。但是在 LSTM 里面，一旦对记忆元造成影响，影响一直会被留着，除非遗忘门要把记忆元的值洗掉。不然记忆元一旦有改变，只会把新的东西加进来，不会把原来的值洗掉，所以它不会有梯度消失的问题。

还有其他技术可以处理梯度消失的问题。比如顺时针循环神经网络或结构约束的循环网络 SCRN 等等