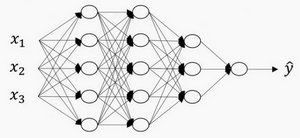
深度神经网络DNN部分原理
DNN
上图是一个四层的神经网络,有三个隐藏层。
用L表示层数,$n^{[l]}$表示第l个隐藏层的神经元数目,$a^{[l]}$来记作l层激活后的结果。用激活函数$g^{[l]}$计算$z^{[l]}$
前向传播和反向传播
前向传播的步骤可以写成
$$
z^{[l]}=W^{[l]}·A^{[l-1]}+b^{[l]}\tag{1}
$$
$$
A^{[l]}=g^{[l]}(Z^{[l]})\tag{2}
$$
前向传播需要喂入$A^{[0]}$也就是$X$,来初始化;初始化的是第一层的输入值。$a^{[0]}$对应于一个训练样本的输入特征,而$A^{[0]}$对应于一整个训练样本的输入特征,所以这就是这条链的第一个前向函数的输入,重复这个步骤就可以从左到右计算前向传播。
反向传播的步骤可以写成
$$
dz^{[l]}=da^{[l]}*g’^{[l]}(z^{[l]})\tag{3}
$$
$$
dw^{[l]}=dz^{[l]}·a^{[l-1]}\tag{4}
$$
$$
db^{[l]}=dz^{[l]}\tag{5}
$$
$$
da^{[l-1]}=dz^{[l]}·W^{[l]T}\tag{6}
$$
向量化表示
$$
dZ^{[l]} = dA^{[l]} * g’^{[l]}(Z^{[l]})\tag{7}
$$
$$
dW^{[l]} = \frac{1}{m} dZ^{[l]} \cdot A^{[l-1]T}\tag{8}
$$
$$
db^{[l]} = \frac{1}{m} np.sum(dZ^{[l]}, axis = 1, keepdims = True)\tag{9}
$$
$$
dA^{[l-1]} = W^{[l]T} \cdot dZ^{[l]}\tag{10}
$$
正向传播是来预测的,反向传播是用来求梯度的,求出来的梯度会用梯度下降法牛顿法等优化方法求解权重w和b,进而用公式$w^{[l]}=w^{[l]}-\alpha dw^{[l]}$,$b^{[l]}=b^{[l]}-\alpha db^{[l]}$更新参数
核对矩阵的维数
实现深度神经网络时,可以拿出一张纸过一遍算法中矩阵的维数来当作检查代码是否有错的方法。
$w$的维度是(下一层的维数,上一层的维数),即$w^{[l]}:(n^{[l]},^{[l-1]})$
$b$的维度是(下一层的维数,1),即$b^{[l]}:(n^{[l]},1)$
$z^{[l]},a^{[l]}:(n^{[l]},1)$
$dw^{[l]}$和$w^{[l]}$维度相同,$db^{[l]}$和$b^{[l]}$维度相同,且$w$和$b$向量化维度不变,但$z,a$以及$x$的维度向量化后会发生变化
向量化后:
$Z^{[l]}$可以看成由每个单独的$Z^{[l]}$叠加而得到,$Z^{[l]}=(z^{[l][1]},z^{[l][2]},z^{[l][3]},…,z^{[l][m]})$
m为训练集大小,所以其维度不再是$(n^{[l]},1)$,而是$(n^{[l]},m)$
$A^{[l]}:(n^{[l]},m)$
在做深度神经网络的反向传播时,一定要确认所有的矩阵维数是前后一致的,可以大大提高代码通过率。